Computer Aptitude Questions – 1’s Complement and 2’s Complement Numbers – set 9
Computer Aptitude Questions – 1’s Complement and 2’s Complement Numbers | Set 9
D.1-5): Convert the following numbers to one’s complement form.
Q.1) Convert the decimal number 45 to one’s complement form.
(a) 101101
(b) 010010
(c) 100010
(d) 010110
(e) 010001
Solution:
b
Step 1:
Convert the given number to binary number.
4510 = 1011012
Step 2: Invest the value of numbers “1 by zero” and “byone”
1011012 → 0100102
Q.2) What is the one’s complement of a number 0111001102?
(a) 100011101
(b) 000011001
(c) 110011001
(d) 100011001
(e) None of these
Solution:
d
011100110 → 100011001
Q.3) What is the one’s complement of a number 10001102
(a) 10110012
(b) 0111101
(c) 0111001
(d) 01100001
(e) 1001001
Solution:
c
1000110 → 0111001
Q.4) What is the one’s complement of a number 2810
(a) 100112
(b) 000012
(c) 110112
(d) 111002
(e) None of these
Solution:
e
Step 1: 2810 → 11100
Step 2: 11100 → 00011
Q.5) What is the one’s complement of a number 5610
(a) 111
(b) 110
(c) 1101
(d) 1111
(e) 000011
Solution:
a
Step 1: Binary conversion
5610 → 111000
Step 2: Invert the digits
111000 → 000111
D.6-10): Convert the following numbers to complemented numbers.
Q.6) 5810
(a) 1001
(b) 111
(c) 110
(d) 010
(e) 1110
Solution:
c
Step 1: Binary conversion => 5810 → 1110102
Step 2: Invert the digits => 111010 → 000101
Step 3: Add 1 with LSB

Q.7)100111012
(a) 01100011
(b) 1101100
(c) 1100010
(d) 1101110
(e) 1100001
Solution:
a
Step 1: Inert the digits
1001 11012 → 01100010
Step 2: Add 1 with LSB

Q.8) 2510
(a) 110
(b) 111
(c) 1101
(d) 100
(e) 101
Solution:
Step 1: Binary conversion: 2510 →11001
Step 2: Invert the digits : 11001 →00110
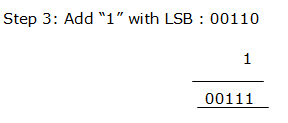
Q.9) 9210
(a) 001100
(b) 101100
(c) 110100
(d) 100100
(e)101011
Solution:
Step 1: Binary conversion: 9210 → 1011100
Step 2: Invert the digits : 1011100 →01000112
Step 3: Add 1 with LSB

Q.10) 110111010112
(a) 111000101
(b) 111010101
(c) 100110101
(d) 110010101
(e) 100010101
Solution:
e
Step 1: Inert the digits
11011101011
Step 2: Add 1 with LSB
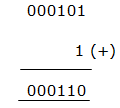


1 comment
Please post questions related to and , or, nor etc,..gate types…