How to Solve Coded inequalities in 10 Seconds : Learn Series

Inequalities Part –II

Introduction:

This article is a continuation of my previous article regarding Direct Inequalities and this article mainly based on the Coded Inequalities problems. So many Aspirants finding difficulties to solve these kind of problems because it’s very time consuming. But, Today I’m going to explain a very simple method and I assure you that it’s possible to solve 5 questions in just two minutes.

Example of Coded Inequality in Reasoning:

Directions: In the following questions, the symbols @, $, %,# and ⋆ are used with the following meaning as illustrated below.

‘A % B’ means ‘A is not smaller than B’.
‘A @ B’ means ‘A is neither smaller than nor equal to B ’.
‘A ⋆ B’ means ‘A is neither greater than nor equal to B’.
‘A $ B’ means ‘A is not greater than B’.
‘A # B’ means ‘A is neither greater than nor smaller than B’.

Now in each of the following questions assuming the given statements to be true, find which of the four conclusions I, II, II and IV given below them is / are definitely true and give your answer accordingly.

Statements:

P $ T, R # T, R % O, K * O

Conclusions:

I. P # K

II. T@K

III.    R # P

IV.   K ⋆ T

V.    O $ P

1) Only either I or II is true
2) Only III and IV are true
3) Only either I or II and III are true
4) Only either I or II and IV are true
5) Only either I or II and III and IV are true

 Follow the steps given below to simplify the process:

In problems on coded inequalities, operators are coded with some symbols. So we first need to decode it and then check the conclusions.

Start decoding symbols one by one
Here symbols are:
% → not smaller than → means greater than or equal to → ‘≥’
@ → neither smaller than nor equal to → means greater than → ‘>’
⋆ → neither greater than nor equal to → means smaller than → ‘<’
$  → not greater than → means smaller than or equal to → ‘≤’
= → neither greater than nor smaller than → means equal to → ‘=’

After decoding the symbol from the given statement then we can understand the meaning of each symbols. Now form a small table to solve the problems.

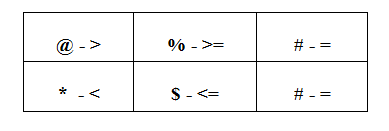
Symbol Priorities:

In Row 1, First priority should go to >. Next >= and = respectively. Likewise,

In Row 2. First priority should go to <. Next <= and =.

Two Direction:

Forward direction

Backward direction

Step 1:  Make sure that your statement parts has a continuity between the entities

• If yes, proceed further
• Else we should modify them continues by inversing the entities and symbols.
  • P $ T, R # T, R % O, K * O
  • P $ T, T # R, R % O, O @ K

Step 2:  Make a single statement

• P $ T # R % O @ K

Step 3: Analyse the conclusions one by one. Always compare with the modified Statement.

P#K

• If you draw a line from P to K, You will move in forward direction.
• Between P and K, The symbols are $,#,% and @.
• If you check these symbols with table #, %, @ are in Row 1 and $ is from Row 2. If we have two row symbols in between the entities then it definitely fails. Hence P#K is False.

T@K

• If you draw a line from T to K, You will move in a forward direction.
• Between T and K, The symbols are #, % and @.
• If you check these symbols with table all the symbols are from Row 1. Highest priority is @. Hence T@K is True.

R#P

• If you draw a line from R to P, You will move in a backward direction.
• Between R and P two symbols are there. One is # and other is $. Both are in Row 2.  Highest priority is $. Since the line moves in backward direction, We should  note the symbol which is exactly opposite or inverse symbol of $ in the table. The opposite symbol of $ is %. But here we have # symbol in our conclusion. Hence, R#P is False.

K*T

• If you draw a line from K to T, You will move in a backward direction.
• Between K and T, The symbols are @ and %. Both are in Row 1. Highest priority is @. Since the line moves in a backward direction, we should note the symbol which is exactly opposite to @ in the table. The opposite symbol of @ is *. Hence K*T is True.

O$P

• If you draw a line from O to P, You will move in a backward direction.
• Between O and P, The symbols are %, # and $.
• If you check these symbols with the table, % is in Row 1 and $ is in Row 2. Hence, the conclusion O$P is False

Other Links to READ

Direct Inequalities Part 1

HOW TO SOLVE PROBLEMS ON PERMUTATIONS-LEARN SERIES

SOLVE PROBLEMS BASED ON AGES

SOLVE PROBLEMS BASED ON AGES