HOW TO SOLVE PROBLEMS ON PERMUTATIONS-LEARN SERIES
Want to Become a Bank, Central / State Govt Officer in 2020?
Join the Most awarded Coaching Institute & Get your Dream Job


Now Prepare for Bank, SSC Exams from Home. Join Online Coure @ lowest fee
Lifetime validity Bank Exam Coaching | Bank PO / Clerk Coaching | Bank SO Exam Coaching | All-in-One SSC Exam Coaching | RRB Railway Exam Coaching | TNPSC Exam Coaching | KPSC Exam Coaching
HOW TO SOLVE PROBLEMS ON PERMUTATIONS-LEARN SERIES
Hi Bankersdaily Aspirants,
IBPS RRB is going to be held shortly and you all know that even 1 mark is important for cracking the competitive exam.Aspirants,Aptitude Section is not that much tough as you think,There is trick to solve each problem in the Aptitude Section.And we are discussing each and every trick and shortcut for solving the Problems in each topic with its Possible Question from the Rudimentry level in which even Neophyte can crack the exam by looking at the article.
Read All Topics by just Single click
INTRODUCTION TO PERMUTATION:
Permutation is defined as the act of arranging all the members of a set into some sequence or order,if the set is already ordered,rearranging its elements,a process called permuting.This topic is also quite easy to solve and it is asked in 1 or 2marks in exam
In general P(n, r) means that the number of permutations of n things taken r at a time. We can either use reasoning to solve these types of permutation problems or we can use the permutation formula.
The formula for permutation is
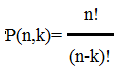
Why we are moving for Permutation:
Lets consider an example:
1) 8 people(A,B,C,D,E,F,G,H) are participating in a Race and there were 3 Prizes Gold, Silver and Bronze .
For Gold the possibility=8 people
For Silver the possibility=7 people
For Bronze the Possibility=6 people
=8*7*6=336
But by using Permutation:(DISTINGUISHABLE ITEMS)
Let us consider we have n items and want to pick k items from it
The Formula P(n,k)
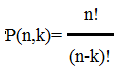
Therefore we have 8 items and we want to pick 3 items
n=8 k=3
=8!/(8-3)! =8*7*6*5*4*3*2*1/5*4*3*2*1 = 8*7*6=336
2)A license plate begins with three letters. If the possible letters are A, B, C, D and E, how many different permutations of these letters can be made if no letter is used more than once?
The problem involves 5 things (A, B, C, D, E) taken 3 at a time.
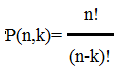
P(5,3)=5!/(5-3)!
=5!/2!
=(5*4*3*2*1)/(1*2)
=5*4*3 =60
There are 60 different permutations for the license plate.
TYPE 2:(INDISTINGUISHABLE ITEMS)
The number of different permutations of n objects where there are n1indistinguishable items, n2 indistinguishable items, … nk
Indistinguishable items, is
![]()
1)How many ways can the letters of the word MATHEMATICS be arranged?
In the Mathematics there are 11 letters in which M occur 2 times, T occur 2 times, A occur 2 times and the remaining word occur only once in the word Mathematics
Total number =11 and there are 3 Repeated Letters(M,T,A)
=11!/(2! *2!*2!) =11*10*9*8*7*6*5*4*3*2*1/(2*1)(2*1)(2*1) = 4989600 ways
TYPE 3 :
PERMUTATION WITH SOME RESTRICTIONS:
(a) Number of permutations of ‘n’ things, taken ‘r’ at a time, when a particular thing is to be always included in each arrangement= r n-1 Pr-1
(b) Number of permutations of ‘n’ things, taken ‘r’ at a time, when a particular thing is fixed: = n-1 Pr-1
(c) Number of permutations of ‘n’ things, taken ‘r’ at a time, when a particular thing is never taken: = n-1 Pr.
(d) Number of permutations of ‘n’ things, taken ‘r’ at a time, when ‘m’ specified things always come together = m! x ( n-m+1) !
(e) Number of permutations of ‘n’ things, taken all at a time, when ‘m’ specified things always come together = n ! – [ m! x (n-m+1)! ]
Example: How many words can be formed with the letters of the word ‘OMEGA’ when:
(i) ‘O’ and ‘A’ occupying end places.
(ii) ‘E’ being always in the middle
(iii) Vowels occupying odd-places
(iv) Vowels being never together.
(i) When ‘O’ and ‘A’ occupying end-places
=> M.E.G. (OA)
Here (OA) are fixed, hence M, E, G can be arranged in 3! ways
But (O,A) can be arranged themselves is 2! ways.
=> Total number of words = 3! x 2! = 12 ways.
(ii) When ‘E’ is fixed in the middle
=> O.M.(E), G.A.
Hence four-letter O.M.G.A. can be arranged in 4! i.e 24 ways.
(iii) Three vowels (O,E,A,) can be arranged in the odd-places (1st, 3rd and 5th) = 3! ways.
And two consonants (M,G,) can be arranged in the even-place (2nd, 4th) = 2 ! ways
=> Total number of ways= 3! x 2! = 12 ways.
(iv) Total number of words = 5! = 120!
If all the vowels come together, then we have: (O.E.A.), M,G
These can be arranged in 3! ways.
But (O,E.A.) can be arranged themselves in 3! ways.
=> Number of ways, when vowels come-together = 3! x 3!
= 36 ways
=> Number of ways, when vowels being never-together
= 120-36
= 84 ways
TYPE 4:
PERMUTATION WITH REPETITION AND WIHTOUT REPETITION:
1.If five digit 1,2,3,4,5 are being given and athree digit code has to be made from it if the repetition of digits is allowed then how many such codes can be formed?
As Repetition is allowed:
We have five options for each digit of the code.Hence, the required number of ways code can be formed is 5*5*5=125
If Repetition is Not Allowed:
1.If three friends are to be chosen from 5 friends (Ajay,Balu,Charan,Dev,Eric) for the party such that Repetition is not allowed then how many it can be done?
If three friends are to be chosen from 5 friends,
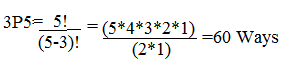
Hence,there are 60 Possible ways to choose 3 friends from 5 friends.
You May Also Like to Read Other Articles:
HOW TO SOLVE PROBLEMS ON AGES -PART 2
HOW TO SOLVE CODED INEQUALITIES IN 10 SECONDS : LEARN SERIES





