LET US SEE HOW TO SOLVE QUADRATIC EQUATION-HOW TO SERIES
Want to Become a Bank, Central / State Govt Officer in 2020?
Join the Most awarded Coaching Institute & Get your Dream Job


Now Prepare for Bank, SSC Exams from Home. Join Online Coure @ lowest fee
Lifetime validity Bank Exam Coaching | Bank PO / Clerk Coaching | Bank SO Exam Coaching | All-in-One SSC Exam Coaching | RRB Railway Exam Coaching | TNPSC Exam Coaching | KPSC Exam Coaching
LET US SEE HOW TO SOLVE QUADRATIC EQUATION-HOW TO SERIES
Hi Bankersdaily Aspirants,
Aspirants today we are going to discuss on the most important topic in Aptitude Section that is Quadratic Equation.Quadratic Equation is asked for 5 marks in Prelims & Mains Examination.This is the easiest section where we can score 5 marks in less than 5 minutes.In this Article we are going to discuss some of the pattern following which Question on Quadratic Equation is asked.
1)BASED ON BASIC QUADRATIC EQUATION
2)BASED ON ROOTS
3)BASED ON FINDING VALUE
#.1.TYPE 1:
BASED ON BASIC QUADRATIC EQUATION:
Find the relationship between X & Y.
1)x²-12x+32=0
y²-7x+12=0
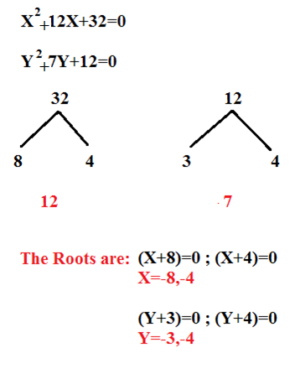
X≤Y
PRACTICE THIS SUM :
1)X²+5X+6=0
Y²+12Y+35=0
2)2X²-10X+12=0
3Y²-12+9=0
#.2. TYPE 2:
BASED ON ROOTS:
This type of Pattern is asked last year in IBPS PO Mains Examination.
1)x²+9√5+100=0
y²-15√8+432=0
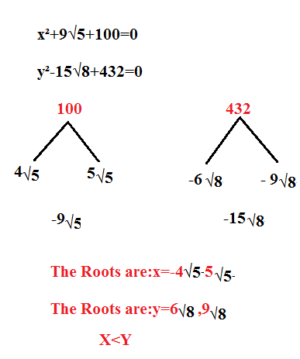
PRACTICE THIS SUM:
1)X²-11√8+240=0
Y²-14√8+360=0
2)X²+11√6+90=0
Y²+15√6+216=0
REMEMBER:
If you Remember this Table then you can answer without Solving,
| SIGN IN THE GIVEN EQUATION | SIGN OF LARGER NUMBER | SIGN OF SMALLER NUMBER |
| +,+ | – | – |
| -,+ | + | + |
| +,- | – | + |
| -,- | + | – |
#.3 TYPE 3:
BASED ON FINDING VALUE:
In this type you will not be given direct value’s you have to find the value from the given statement and find the relationship between them.Let see with an example,
X=Area of Square whose Side is 4cm
Y=Area of Equilateral Triangle whose side is 8cm
X=Area of Square=4²=16 Sq.cm
Y=Area of Equilateral Triangle √3/4 * 8² = 16√3 Sq.cm
Therefore X<Y.
PRACTICE THIS SUM:
1)X=Area of Triangle whose base is 1.5cm and height is 75cm
Y=Area of the equilateral triangle whose side is 12 cm
2)X=length of the diagonal of a square whose area is 400 sq.m
Y=Perimeter of a Square Plot whose area is 400 sq.m






4 comments
Unable to check the answers
Sir, How to check equation using the above table. Give some example
Unable to check the answer by click check your answer. it is not shown. tricks are nice easy to pick answer. thank you
Hi Sir,
Sir for me its working properly,Pls refresh your page.If again it doesn’t work let me know it