PROBLEMS ON PROBABILITY:PART 2-HOW TO SERIES
Want to Become a Bank, Central / State Govt Officer in 2020?
Join the Most awarded Coaching Institute & Get your Dream Job


Now Prepare for Bank, SSC Exams from Home. Join Online Coure @ lowest fee
Lifetime validity Bank Exam Coaching | Bank PO / Clerk Coaching | Bank SO Exam Coaching | All-in-One SSC Exam Coaching | RRB Railway Exam Coaching | TNPSC Exam Coaching | KPSC Exam Coaching
PROBLEMS ON PROBABILITY:PART 2-HOW TO SERIES
Hi Bankersdaily Aspirants,
Learning is a step by step process and you should gradually progress in that to ace the process. As you all know we have started a new How to Series to help with your preparations for various exams like IBPS PO , IBPS RRB Scale I officer , IBPS RRB Office Assistant , IBPS Clerk , IBPS SO , SBI PO , SBI Clerk , SBI SO and many other exams in this type.
Friends as I always say to ace in the exam we don’t want to get Cent Percentage, we just want to get the cut off mark in the exam.It is not that much difficult to get the cut off mark.There is certain topic in the Aptitude Section which we can solve in less than a minute & PROBABILITY is one among that.If you have practiced this topic then you can solve this with in a minute.We had already discussed some of the types of questions in Previous Article(Probability Part 1).Today we will discuss another set of question in this article.Before that have a glance of Part 1
1)BASED ON CARDS
2)BASED ON BALLS
#.1.TYPE 1:
BASED ON CARDS:
Friends in the last Article we had discussed problems on cards with the Keyword Both.In this Article we will discuss problems based on the Keyword
No, One from one type & Another from another type
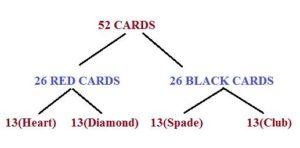
13 Cards in Diamond,Heart,Spade & Club Contains:
Numbered Card:2,3,4,5,6,7,8,9,10(Totally 9 Numbered Cards)
Face Card:There are 4 Face Card they are (ACE,KING QUEEN & JACK)
9+4=13 CARDS in each Suit.
Now let us look into the Problem.
1)When 1 card is drawn at Random,What is the Probability that there will be NO King Card?
Probability=Number of Possible Ways/Total Number of Events
Here we are going to draw 1 card therefore the Total number of Events or Sample Space=52C1=52
There are 4 King Cards in 52 Cards
1 from Diamond,1 from Heart,1 from club,1 from Spade,Totally 4 King Cards in 52 Cards.
=52-4=48
Therefore Possible ways=48C1
Probability of getting No King:
![]()
=48/52
=12/13
2)When three cards are drawn,What is the Probability that one card is Ace,one Card is King & one card is Jack?
Friends shall we solve together,
3 Cards are drawn,Total Possibility=52C3=52*51*50/1*2*3
=26*17*50
Now,let us find the Possible Number of ways of getting 1 Ace,1 King & 1 Jack
There are 4 Ace in 52 Cards,
1 King in 52 Cards,
1 Jack in 52 Cards,
Now,we have to choose 1 card from each face.
4C1 * 4C1 * 4C1=4*4*4
Therefore,
=4*4*4/ 26*17*50
Probability of getting 3 Cards=16/5525
#.2.TYPE 2:
BASED ON BALLS:
In this type,Questions will be asked in such a way that certain balls are drawn in different colours and after that there will be two conditions after this
1)They were Replaced.
2)They were not Replaced.
1)THEY WERE REPLACED:
A bag contains 8 Red & 10 Black Balls.If two draws of three balls are drawn randomly & the balls are replaced after the first draw then what is the probability that three balls are Red Balls at the first draw and Black Balls at the Second Draw?
A Bag Contains 8 Red & 10 Black Balls
At First Draw:
They will draw three balls of Red Colour,
Number of Possible ways=8C3(Since 3 Red Balls are to be drawn from 8 Red Balls)
Total Number of Ways=18C3(Since 3 Red Balls are to be drawn from 18 Balls)
We all know the formula to find the Probability,
=Number of Possible Ways/Total Number of Ways
=8C3/18C3
8C3=8*7*6/1*2*3=56
18C3=18*17*16/1*2*3=816
=56/816
Probability of the First Draw=7/102
At Second Draw:
We want to draw 3 Balls from 10 Black Balls
Possible Ways=10C3=10*9*8/1*2*3=120
Total Number of Ways=18C3=18*17*16/1*2*3=816
Probability=120/816=5/34
Probability of the Second Draw:5/34
Total Probability=7/102 * 5/34
We had Used * here Do You know why?
Because In the Question they ask us to find the Probability of First Draw & Second Draw
And is Used So we have to Multiply it,
If they said to Find First Draw or Second Draw then We would add it .
Note:If “AND” is represented in the question then we have to “Multiply” the term.
If “OR” is represented in the question then we have to “Add” the term.
2)Without Replacement:
A Bag Contains 8 Red Balls & 10 Black Balls.Four Balls are Drawn one by one & they are not replaced.Find the Probability if the balls drawn are of Alternate of different Colours?(That is,if 1st ball is Red 2nd would be Black …,Vice Versa)
Let us Assume if 1st Ball Drawn of Red Colour then,
Probability of 1st Ball:
Possible Ways=8C1=8
Total Ways=18C1=18
Probability of First Ball=8/18=4/9
Since the Ball is not Replaced,now there will be 7Red Balls & Black Balls Remain the Same Totally 17 Balls
Probability of 2nd Ball(That is Black):
Possible Ways=10C1=10
Total Ways=17C1=17
Probability of Second Ball=10/17
This Ball will also be not Replaced then there will be 7Red Balls 9 Black Balls & the Total number of Balls=16 balls
Probability of Third Ball:(Red)
Possible Ways=7C1=7
Total Ways=16C1=16
Probability of Third Ball=7/16
This Ball also will not be replaced then there will be 6 Red balls & 9 Black Balls & the total number of Balls=15 Balls
Probability of Fourth Ball(Black)
Possible Ways=9C1=9
Total Ways=15C1=15
Probability of Fourth Ball=9/15=3/5
Since we want all the Four ball(AND) Therefore we must Multiply individual Probability
4/9 * 10/17 * 7/16 * 2/5
Probability of drawing 4 balls alternatively( if we start with Red Ball)=7/102
Probability of drawing 4 balls alternatively(if we start with Black Ball):
First Ball(Black)=10/18=5/9
Second Ball(Red)=8/17
Third Ball(Black)=9/16
Fourth Ball(Red)=7/15
When Four Balls are drawn the Probability is=7/102
Now the Probability is First Ball May be RED or Second Ball May be BLACK
Now we have to add because the Term OR is used
7/102 + 7/102 =14/102=7/51
Friends I think this Article would help you to get an Idea About Probability.
If you have any Query Don’t Hesitate to Post your Query in the Comment Box we will Respond you as soon as possible
RELATED ARTICLE:
IBPS PO PREVIOUS YEAR CUTOFF MARKS – PRELIMS
IB ACIO 2017 – EXAM PATTERN AND LAST DATE EXTENDED



