Practice Questions – Permutation and Combination – 1
1) Find the value of 9P3.
(a) 504
(b) 309
(c) 405
(d) 600
Click here to view Answer
(a) 504
Explanation:
9P3 = 9!/6!
Because, nPr
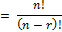
= (9 ×8 ×7 ×6!)/6!
= 9 × 8 × 7 = 504
2) Find the value of n, if nP5 = 20 nP3.
(a) 5
(b) 8
(c) 6
(d) 4
Click here to view Answer
(b) 8
Explanation:
nP5 = 20 nP3
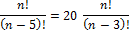
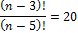
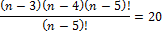
(n – 3)(n – 4) = 20
n = 8 (n = -1 is inadmissible)
3) How many numbers greater than 5000 can be formed with the digits, 3, 5, 7, 8, 9 no digit being repeated?
(a) 216
(b) 126
(c) 512
(d) 252
Click here to view Answer
(a) 216
Explanation:
= 4 × 4 × 3 × 2 = 96
Thousands place cannot assume 3 since required numbers are greater than 5000.
= 5 × 4 × 3 × 2 × 1 = 120
Total required numbers = 96 + 120 = 216.
4) How many 6 digit telephone numbers can be constructed with the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 if each number starts with 35 and no digit appears more than once?
(a) 1600
(b) 1680
(c) 900000
(d) 9000
Click here to view Answer
(b) 1680
Explanation:
= 8 × 7 × 6 × 5 = 1680
3 and 5 have been already used, so we have 8 digits for thousands place, then 7 digits for hundreds place, 6 digits for tens digit and remaining 5 digits for unit place.
5) How many 6 digit numbers can be formed from the digits 1, 2, 4, 5, 6, 7 (no digit being repeated) which are divisible by 5?
(a) 555
(b) 156
(c) 120
(d) None of these
Click here to view Answer
(c) 120
Explanation:
A number is divisible by 5 only if its unit digit is either 5 or 0. So we fix 5 as unit digit and then we fill up the remaining places.
= 5 × 4 × 3 × 2 × 1 = 120
Hence, required number is 120.
6) How many even numbers greater than 300 can be formed with the digits 1, 2, 3, 4, 5 no digit being repeated?
(a) 111
(b) 600
(c) 900
(d) None of these
Click here to view Answer
(a) 111
Explanation:
Case 1
= 3 × 3 × 1 = 9
When 2 is fixed at unit place, we have 3, 4 and 5 i.e., 3 digits for hundreds place and remaining 3 digits (out of 5) for the tens place.
= 2 × 3 × 1 = 6
When 4 is fixed at unit place, we have 3 and 5 i.e., only two digits for hundreds place and remaining 3 digits for tens place.
Case 2
= 48
Case 3
= 48
5 digit numbers = 48
Thus there are total 15 + 48 + 48 = 111 even numbers greater than 300.
7) In how many ways the letters of the word RAINBOW be arranged?
(a) 5040
(b) 4050
(c) 3040
(d) 8040
Click here to view Answer
(a) 5040
Explanation:
There are 7 letters in the word RAINBOW and each letter is used only once. So all the 7 letters can be arranged in 7! Ways.
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
8) In the word RAINBOW, how many words begin with R?
(a) 720
(b) 360
(c) 1440
(d) None of these
Click here to view Answer
(a) 720
Explanation:
If we fix R as initial letter, then we have to arrange only 6 remaining letters.
Hence required number of permutations = 6!
= 6 × 5 × 4 × 3 × 2 × 1 = 720
9) In the word RAINBOW, how many words begin with R and ends with W?
(a) 120
(b) 240
(c) 180
(d) 360
Click here to view Answer
(a) 120
Explanation:
If we fix R and W as the first and last letters then we have to arrange only 5 remaining letters which can be arranged in 5! = 120 ways.
10) In the word RAINBOW, how many words are there in which I and O are never together?
(a) 1440
(b) 720
(c) 3600
(d) None of these
Click here to view Answer
(c) 3600
Explanation:
Number of permutations when I and O are together
= 2! × 6! = 1440
Total number of permutations = 7! = 5040
Therefore, number of permutations when I and O are not together
= 5040 – 1440 = 3600



