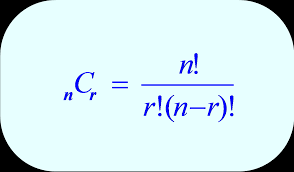PRACTICE QUIZ ON PROBLEMS BASED ON PERMUTATIONS
Want to Become a Bank, Central / State Govt Officer in 2020?
Join the Most awarded Coaching Institute & Get your Dream Job


Now Prepare for Bank, SSC Exams from Home. Join Online Coure @ lowest fee
Lifetime validity Bank Exam Coaching | Bank PO / Clerk Coaching | Bank SO Exam Coaching | All-in-One SSC Exam Coaching | RRB Railway Exam Coaching | TNPSC Exam Coaching | KPSC Exam Coaching
PRACTICE QUIZ ON PROBLEMS BASED ON PERMUTATIONS
Hi Bankersdaily Aspirants,
Aspirants,As you all know that IBPS RRB is going to held shortly,we are in the right time for our preparation.Keeping Neophyte in mind we are discussing each topic in Aptitude Section.
You may also like to Read Articles on:
THINGS TO CONSIDER WHILE PREPARING FOR IBPS RRB PRELIMS
PRACTICE QUIZ ON AGES-LEARN SERIES
LET US ATTEMPT QUIZ BASED ON TRAINS